Consequences of Nyquist
Theorem for Acoustic Signals Stored in Digital Format
by Marek Roland-Mieszkowski, M.Sc., Ph.D., Digital
Recordings and
Wayne R. Young, School of Human Communication Disorders, Dalhousie University,
Halifax, Nova Scotia, Canada
This paper was published in proceedings from "Acoustic Week in Canada 1991" -
CAA Conference, Edmonton, Alberta, Canada, October 7 - 10, 1991
Copyright 1991-2014, Digital Recordings. All Rights Reserved.

Content
Introduction
The calculation of functions in digital domain from analogue acoustic
signals involves a two-step process which includes analog to digital
(A/D) conversion and digital calculations performed on digitized
acoustical signal. Function V(t) will be represented digitally without
any loss of information as long as sampling occurs in accordance
with the Nyquist criteria [1-9]. How can we determine the values of
digitized function for points between samples when we have only N
samples available? The Nyquist formula requires an infinite
number of samples to accomplish this task. In situations when
digital samples are sufficiently dense, one can approximate many
continuous functions with their discrete formulations. Errors
generated in these cases will be small, since they depend on spacing
between samples. The situation will be different, however, when
samples are coarsely spaced. For example, a sinusoidal tone of
frequency f = 20,000 Hz sampled at fsampling = 44,100 Hz is
represented
by only 2.205 samples per period. Calculation of many functions
(for example RMS values) may lead in this case to some errors.
Finite duration sampling of continuous signal results in errors caused
by our limited knowledge of the function for all points in time. It
turns out that the more samples we have around the region of interest,
the more accurately we are able to reproduce the function there. This
paper investigates the error caused by truncation of the Nyquist
sampling formula with the aim of quantifying it and establishing
ways to minimize its effect.
Back to the Content
Nyquist Theorem
According to the Nyquist theorem [1-9] the discrete time sequence of
a sampled continuous function { V(tn = n  Ts) } contains enough
information to reproduce the function V=V(t) exactly provided that
the sampling rate (fs = 1/Ts) is at least twice that of the highest
frequency contained in the original signal V(t): Ts) } contains enough
information to reproduce the function V=V(t) exactly provided that
the sampling rate (fs = 1/Ts) is at least twice that of the highest
frequency contained in the original signal V(t):
![[Nyquist Theorem]](r01_1.gif) |
(1) |
where:
fS = 1/TS -- sampling frequency
V(t) -- value of signal (voltage) at arbitrary time t
V[n] = V(n  TS) -- value of signal at time t = n TS) -- value of signal at time t = n
 TS TS
Back to the Content
Nyquist Theorem's Consequences
It is worth noting that information about the signal V = V(t) at any
given moment in time t 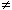 n n  TS is distributed
among all discrete
samples { V[n] } with appropriate weights ( see eq. (1) ).
Realistically, we are never presented with an infinite discrete time
sequence and are therefore forced to perform the summation over a
finite range. This is equivalent to a loss of information about the
function V = V(t) not only before and after our time window (which
is understandable), but also at the time points between the sampling
points. This can introduce errors into the process of reconstructing
the function. Let assume that we have available to us N digital
samples of function V = V(t) (this is illustrated in Figure 1): TS is distributed
among all discrete
samples { V[n] } with appropriate weights ( see eq. (1) ).
Realistically, we are never presented with an infinite discrete time
sequence and are therefore forced to perform the summation over a
finite range. This is equivalent to a loss of information about the
function V = V(t) not only before and after our time window (which
is understandable), but also at the time points between the sampling
points. This can introduce errors into the process of reconstructing
the function. Let assume that we have available to us N digital
samples of function V = V(t) (this is illustrated in Figure 1):
V[n] = V(n  TS) where n = 0,1,2,...,(N-1) TS) where n = 0,1,2,...,(N-1) |
(2) |
![[Nyquist Theorem]](n01.gif)
![[Nyquist Theorem]](n01_1.gif)
Figure 1: Illustration of available values V[n] in the time window
[0, (N-1)  TS] TS]
Values of the function V = V(t) for the times t 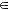 [ 0
[ 0  TS ; (N-1) TS ; (N-1)  TS],
can be estimated by a truncated version of formula (1) : TS],
can be estimated by a truncated version of formula (1) :
![[Nyquist Theorem]](r01_2.gif) |
(3) |
The errors resulting from truncation are 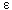 LEFT(t)
and LEFT(t)
and 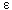 RIGHT(t).
They represent the "LEFT" and "RIGHT" portions of the sum
(with respect to the time axis) in eq. (1) that are omitted in eq.(3),
and can be represented mathematically by the following formulas : RIGHT(t).
They represent the "LEFT" and "RIGHT" portions of the sum
(with respect to the time axis) in eq. (1) that are omitted in eq.(3),
and can be represented mathematically by the following formulas :
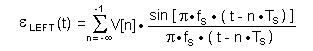 |
(4a) |
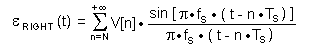 |
(4b) |
The sum truncation error is generated when eq.(3) is used instead of
eq.(1), and is given by the following formula:
 TOTAL(t) = TOTAL(t) =  LEFT(t) + LEFT(t) +
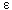 RIGHT(t) RIGHT(t) |
(5) |
where:
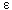 LEFT(t) -- "LEFT" error (due to truncation to the
left where values of V[n] are unknown) LEFT(t) -- "LEFT" error (due to truncation to the
left where values of V[n] are unknown)
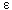 RIGHT(t) -- "RIGHT" error (due to truncation to the
right where values of V[n] are unknown) RIGHT(t) -- "RIGHT" error (due to truncation to the
right where values of V[n] are unknown)
In the next section we will try to evaluate the sum truncation error for
different cases.
Back to the Content
Evaluation of Sum Truncation Error
If a priori information is given, that V(t) = 0
for t 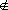 [0 ; (N-1)TS]
then [0 ; (N-1)TS]
then 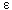 TOTAL = 0
(since TOTAL = 0
(since 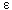 LEFT = 0 and LEFT = 0 and 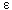 RIGHT
= 0) and we can
use with
full confidence the truncated version of the Nyquist sum ( eq. (3) ).
Otherwise using the sum from eq. (3) is equivalent to the zero-extension
(or zero-padding) method [3,5]. RIGHT
= 0) and we can
use with
full confidence the truncated version of the Nyquist sum ( eq. (3) ).
Otherwise using the sum from eq. (3) is equivalent to the zero-extension
(or zero-padding) method [3,5].
If a priori information is given, that function
V = V(t) is periodic
( ie. V(t) = V(t + T) ) then this information can be used in
formula
(1). In the special case when the function period T= N0  TS, where
N0
TS, where
N0 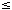 N, one can use formula (1) directly since all values
of function
V[n] are known for n N, one can use formula (1) directly since all values
of function
V[n] are known for n 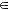 (- (- 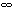 ;
+ ;
+ 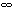 ). In this case one can also use the
Discrete Fourier Transform ( DFT) on N0 consecutive data points
(from the available N data points V[n] where n=0,1,2.....(N-1) ) to
calculate amplitudes Ai , and phases ). In this case one can also use the
Discrete Fourier Transform ( DFT) on N0 consecutive data points
(from the available N data points V[n] where n=0,1,2.....(N-1) ) to
calculate amplitudes Ai , and phases 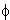 i,
of the periodic signal and
then use the formula : i,
of the periodic signal and
then use the formula :
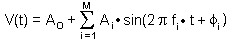 |
(6) |
where:
A0 -- DC component of the periodic signal V = V(t)
Ai -- amplitudes calculated from DFT
 i -- phases calculated from DFT i -- phases calculated from DFT
fi = ( i / N0)  fS -- frequencies
available in periodic signal V = V(t) fS -- frequencies
available in periodic signal V = V(t)
M = INT ( N0 / 2 ) -- number of the highest possible harmonic (since
fi  fS / 2) fS / 2)
When a priori information is not available about
the function
V = V(t) then direct use of the truncated Nyquist sum
( eq. (3) ) is
going to lead to truncation error  TOTAL given by eq. (4)
and (5).
Values V[n] in eq. (4 a) and (4 b) can be any arbitrary numbers,
since we do not have any a priori information about the signal. In the
next section we will investigate this in greater detail to estimate
values of possible errors. TOTAL given by eq. (4)
and (5).
Values V[n] in eq. (4 a) and (4 b) can be any arbitrary numbers,
since we do not have any a priori information about the signal. In the
next section we will investigate this in greater detail to estimate
values of possible errors.
Back to the Content
Estimation of Truncation Error for General Case
Let's consider for simplicity the "LEFT" error given by eq. (4 a)
(estimation of "RIGHT" error is performed in identical way). Total
error given by eq. (4 a) is a sum of contributions from data points
V[n] where n=-1,-2,-3.........- 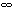 . .
Error contribution from the n-th point is given by :
 |
(7) |
where:
t  [ 0 ; (N-1) [ 0 ; (N-1)  TS] TS]
n = -1, -2, -3, . . . ,- 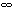 for "LEFT" errors for "LEFT" errors
n = N, (N+1), . . . , +  for "RIGHT" errors for "RIGHT" errors
The function sin(x) / x ( where x= 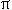  fS fS
 (t - n (t - n  TS) ) is equal to 0 at
time points t = m TS) ) is equal to 0 at
time points t = m  TS; m = 0,1,2,3, . . . ,(N-1) (which are the
sampling
points in our time window). Therefore there is no contribution to the
error in V(t) at sampling points due to truncation. Also the function
sin (x) / x has local max. and min. approximately at the middle points
between adjacent sampling points in our time window. This can be
proved easily by taking first derivative of function sin(x) / x. The
approximation gets better for larger values of x. Therefore from now
on we will consider the error at the middle points between samples
V[n] in our time window (see fig.1.) : TS; m = 0,1,2,3, . . . ,(N-1) (which are the
sampling
points in our time window). Therefore there is no contribution to the
error in V(t) at sampling points due to truncation. Also the function
sin (x) / x has local max. and min. approximately at the middle points
between adjacent sampling points in our time window. This can be
proved easily by taking first derivative of function sin(x) / x. The
approximation gets better for larger values of x. Therefore from now
on we will consider the error at the middle points between samples
V[n] in our time window (see fig.1.) :
t = ( m + 1/2 )  TS TS |
(8) |
Substituting time t from eq (8) into formula (7) we get:
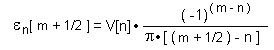 |
(9) |
where:
m = 0, 1, 2, 3, ... , (N-2) -- indexing of middle points between adjacent samples
in the time window
n = -1, -2, -3, ... , - -- indexing of points on the left
of the time window (see fig.1) -- indexing of points on the left
of the time window (see fig.1)
An interesting question to ask is how large the value of index
"m" in eq.(9) must be in order for the absolute value of error
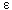 -1[m+1/2] to be equal or smaller than 1/2 of the
quantization step -1[m+1/2] to be equal or smaller than 1/2 of the
quantization step 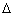 , which is defined as a difference between quantization
levels
[1,3,8,9]. This is a reasonable comparison since all samples V[n]
have quantization error inherent to the process of A/D conversion
[1,3,8,9]. Quantization error is uniformly distributed in the range
[- , which is defined as a difference between quantization
levels
[1,3,8,9]. This is a reasonable comparison since all samples V[n]
have quantization error inherent to the process of A/D conversion
[1,3,8,9]. Quantization error is uniformly distributed in the range
[-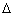 /2 ; /2 ; 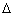 /2 ], where /2 ], where 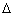 is a step size in the
A/D converter [1,3,8,9].
From eq. (9) we have for n=-1 and V[-1] = VMAX = 2B-1 is a step size in the
A/D converter [1,3,8,9].
From eq. (9) we have for n=-1 and V[-1] = VMAX = 2B-1
 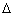 (where
VMAX is the max. possible signal amplitude in the A/D converter and
B is the No. of bits in the A/D converter) : (where
VMAX is the max. possible signal amplitude in the A/D converter and
B is the No. of bits in the A/D converter) :
m 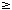 2B / 2B / 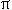 - 3/2 - 3/2 |
(10) |
From inequality (10) we get (times are calculated for fS = 44,100 Hz):
| for B = 8 bit |
m 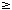 80 80 |
( 0.001 sec inside sound file ) |
|
| for B = 10 bit |
m 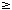 325 325 |
( 0.007 sec inside sound file ) |
|
| for B = 12 bit |
m 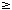 1,303 1,303 |
( 0.030 sec inside sound file ) |
|
| for B = 14 bit |
m 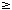 5,214 5,214 |
( 0.118 sec inside sound file ) |
(11) |
| for B = 16 bit |
m 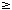 20,860 20,860 |
( 0.473 sec inside sound file ) |
|
| for B = 18 bit |
m 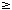 83,442 83,442 |
( 1.892 sec inside sound file ) |
|
| for B = 20 bit |
m 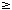 333,771 333,771 |
( 7.569 sec inside sound file ) |
|
Update for DVD Audio/Video format (July 2000)
|
| for B = 24 bit |
m 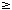 5,340,352 5,340,352 |
( 121.096 sec inside sound file -- 44.1 kHz sampling) |
|
| for B = 24 bit |
m 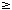 5,340,352 5,340,352 |
( 55.629 sec inside sound file -- 96 kHz sampling) |
|
| for B = 24 bit |
m 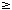 5,340,352 5,340,352 |
( 27.814 sec inside sound file -- 192 kHz sampling) |
|
Results in (11) show that if we have no information about the signal
before our time window, then in order to avoid errors associated with
the unknown values of function V[-1], V[-2], V[-3]........, one has to
be " m" samples deep inside of the time window. We can then use the
formula (3) for any time t as long as we stay away from the ends of
the time window by " m " samples ( t 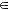 [ m [ m  TS ; (N-1-m)
TS ; (N-1-m)  TS ] ). TS ] ).
Another interesting question to ask is which sequence of samples
V[-1], V[-2], V[-3]........will generate the largest error at the middle
points in our time window ? Taking the summation of eq. (9) from
n = -1 to m = -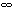 we get : we get :
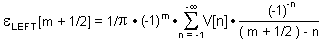 |
(12) |
If we take the sequence of samples V[n] = VMAX  (-1)n
then we get from eq (12) : (-1)n
then we get from eq (12) :
 |
(13) |
Unfortunately our choice of { V[n] } in eq. (13) was inappropriate
because the sum of this series diverges to 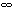 .
As a matter of fact this
happened since this particular series corresponds to the digital
representation of a sine wave with the Nyquist frequency f = fS / 2.
Such a frequency can't exist in the digital domain, since it can't be
recorded via A/D conversion. A realizable choice of samples would
be, for example, one which represents sinusoidal wave with
frequency f .
As a matter of fact this
happened since this particular series corresponds to the digital
representation of a sine wave with the Nyquist frequency f = fS / 2.
Such a frequency can't exist in the digital domain, since it can't be
recorded via A/D conversion. A realizable choice of samples would
be, for example, one which represents sinusoidal wave with
frequency f  fS / 2 : fS / 2 :
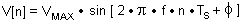 |
(14) |
where:
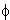 = = 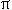 / 2 + 2 / 2 + 2  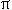
 f f  TS - phase angle chosen to maximize error
for n = -1 ( V[n = -1] = VMAX TS - phase angle chosen to maximize error
for n = -1 ( V[n = -1] = VMAX
Substituting (14) in eq. (12) we get:
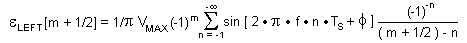 |
(15) |
Computer calculations of error were performed using formula (15)
for m = 10,000 (calculations of error in middle point between 10,000 and
10,001 sample in time window) . Results were as follows :
for f = 0.250  fs fs |
S(1) = 3.18 E-04  VMAX VMAX |
S(10,000) = 1.45 E-04  VMAX VMAX |
|
for f = 0.300  fs fs |
S(1) = 3.18 E-04  VMAX VMAX |
S(10,000) = 1.45 E-04  VMAX VMAX |
|
for f = 0.350  fs fs |
S(1) = 3.18 E-04  VMAX VMAX |
S(10,000) = 1.45 E-04  VMAX VMAX |
|
for f = 0.400  fs fs |
S(1) = 3.18 E-04  VMAX VMAX |
S(10,000) = 1.45 E-04  VMAX VMAX |
(16) |
for f = 0.450  fs fs |
S(1) = 3.18 E-04  VMAX VMAX |
S(10,000) = 1.48 E-04  VMAX VMAX |
|
for f = 0.490  fs fs |
S(1) = 3.18 E-04  VMAX VMAX |
S(10,000) = 2.24 E-04  VMAX VMAX |
|
for f = 0.499  fs fs |
S(1) = 3.18 E-04  VMAX VMAX |
S(10,000) = 7.23 E-04  VMAX VMAX |
|
where:
S(1) represents first term in eq.(15) (contribution from the V[-1 ] )
S(10,000) represents summation of first 10,000 terms in eq. (15)
Results (16) show, that max. error is obtained when frequency f
approaches the Nyquist frequency fS / 2. The value of the error from
the first term ( V[-1] ) is larger than from the sinusoidal wave as long
as frequency f is smaller than about 0.490  fS
( which is 98% of
Nyquist frequency = fS / 2 ). This seems reasonable since the input
antialiasing filter would usually eliminate all frequencies above
0.46 fS
( which is 98% of
Nyquist frequency = fS / 2 ). This seems reasonable since the input
antialiasing filter would usually eliminate all frequencies above
0.46  fS (see for example data for PCM or DAT recorders).
The errors
resulting from sinusoidal waves are similar to the error contribution
from V[-1], therefore we expect that the recommendation given in
(11) should be valid for any arbitrary sequence V[-1],V[-2],V[-3] ..,
since such sequence is a linear combination of pure tones according
to the Fourier Theorem. However, further investigation and computer
simulations are required to substantiate this claim. fS (see for example data for PCM or DAT recorders).
The errors
resulting from sinusoidal waves are similar to the error contribution
from V[-1], therefore we expect that the recommendation given in
(11) should be valid for any arbitrary sequence V[-1],V[-2],V[-3] ..,
since such sequence is a linear combination of pure tones according
to the Fourier Theorem. However, further investigation and computer
simulations are required to substantiate this claim.
Back to the Content
Conclusions
In this paper we investigated the errors due to finite duration
sampling of continuous signal and determined that this error can be
considerable at the beginning and near the end of the sampling time
window. These errors had a tendency to get larger at higher
frequencies as they approach the Nyquist frequency ( fS / 2) for signal
near the inside boundaries of the time window. At this time
however, we don't know which physically realizable sequence of
samples V[-1], V[-2], V[-3]..........will produce the largest error inside
of the time window. Further tests and computer simulations are
required.
Back to the Content
|
Use CD-CHECK to test error
correction and
tracking capability of a CD / DVD player
|
|
|
Use DED for continuous monitoring
of the digital output signal and the digital link from CD / DVD
players, DAT recorders and other digital sources
|
|
References
- [1] Nakajima et al., "The Sony Book of Digital Audio Technology",
published by TAB Books Inc.,1983.
- [2] Papoulis Athanasios, "Circuits and Systems, A Modern
Approach", Holt, published by Rinehart and Winston Inc.,1980.
- [3] Oppenheim Alan V., Schafer Ronald W., "Discrete-Time Signal
Processing", published by Prentice Hall Inc., 1989.
- [4] Jayant N. S., Noll Peter, "Digital Coding of Waveforms,
Principles and Applications to Speech and Video", published by
Pretice-Hall Inc., 1984.
- [5] Jackson Leland B., "Digital Filters and Signal Processing",
published by Kluwer Academic Publishers, 1989.
- [6] Press William et al., "Numerical Recipes", published by
Cambridge University Press, 1987.
- [7] Weaver H. Joseph, "Applications of Discrete and Continuous
Fourier Analysis", published by John Wiley & Sons, 1983.
- [8] Marek Roland-Mieszkowski, "Introduction to Digital Recording
Techniques", Proceedings from "Acoustic Week in Canada 1989" -
CAA Conference,Halifax,N.S.,Canada,October 16-19,1989, 73-77.
- [9] Robert Wannamaker, Stanley Lipshitz and John Vanderkooy,
"Dithering to eliminate quantization distortion", Proceedings from
"Acoustic Week in Canada 1989" - CAA Conference, Halifax, N.S.,
Canada, October 16-19, 1989, pp. 78-86.
Back to the Content
Terms of Use |
Return Policy |
Privacy Policy
Copyright (©) 1989-2014 by Digital Recordings. All Rights Reserved.
No part of the information provided on this www page may be
reproduced for any purpose,
in any form, without prior written approval.
|
This site uses frames. To enjoy them your screen's resolution should be
at least 800 x 600, preferably 1024 x 768. To invoke frames click
here.
|
|
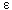 LEFT(t) -- "LEFT" error (due to truncation to the
left where values of V[n] are unknown)
LEFT(t) -- "LEFT" error (due to truncation to the
left where values of V[n] are unknown)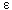 RIGHT(t) -- "RIGHT" error (due to truncation to the
right where values of V[n] are unknown)
RIGHT(t) -- "RIGHT" error (due to truncation to the
right where values of V[n] are unknown)
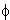 i -- phases calculated from DFT
i -- phases calculated from DFT fS / 2)
fS / 2)
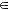 [ 0 ; (N-1)
[ 0 ; (N-1) 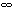 for "LEFT" errors
for "LEFT" errors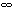 for "RIGHT" errors
for "RIGHT" errors
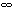 -- indexing of points on the left
of the time window (see fig.1)
-- indexing of points on the left
of the time window (see fig.1)
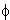 =
= 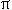 / 2 + 2
/ 2 + 2 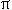
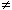 n
n ![[Nyquist Theorem]](n01.gif)
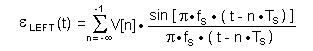
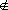 [0 ; (N-1)TS]
then
[0 ; (N-1)TS]
then  N, one can use formula (1) directly since all values
of function
V[n] are known for n
N, one can use formula (1) directly since all values
of function
V[n] are known for n 
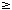 2B /
2B /